Answer:
The standard deviation of your weight over a day is of 1.1547 pounds.
Explanation:
Uniform probability distribution:
An uniform distribution has two bounds, a and b, and the standard deviation is:
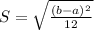
Assume that the changes in water weight is uniformly distributed between minus two and plus two pounds in a day.
This means that

What is the standard deviation of your weight over a day?
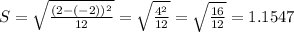
The standard deviation of your weight over a day is of 1.1547 pounds.