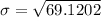Answer:
The right answer is:
(a) 0.1456
(b) 18.125, 69.1202, 8.3139
Explanation:
Given:
N = 24
n = 5
r = 7
The improperly drilled gearboxes "X".
then,
⇒
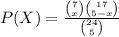
(a)
P (all gearboxes fit properly) =
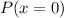
=
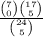
=
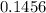
(b)
According to the question,
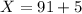
Mean will be:
⇒

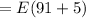

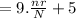
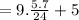
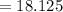
Variance will be:
⇒
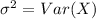
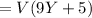
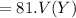
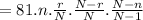
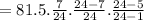
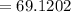
Standard deviation will be:
⇒