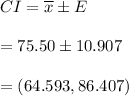Answer:
The t value for 99% CI for 21 df is 2.831.
The critical value that should be used in constructing the confidence interval is (64.593, 86.407).
Explanation:
Now the sample size is less than 30 and also population standard deviation is not known.
Then we will use t distribution to find CI
t value for 99% CI for 21 df is TINV(0.01,21)=2.831
The margin of error is
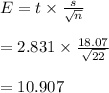
Hence CI is