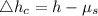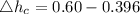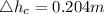Answer:
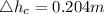
Step-by-step explanation:
Diameter
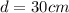
Height
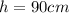
Fill height
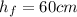
Angular speed
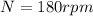
Generally the equation for Angular velocity is mathematically given by
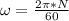
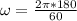
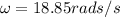
Generally the equation for Liquid surface is mathematically given by
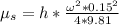
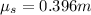
Therefore the liquid drop at center due to rotation is