Answer:
Since
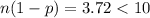 , the normal curve cannot be used as an approximation to the binomial probability.
, the normal curve cannot be used as an approximation to the binomial probability.
100% probability that greater than 26 out of 124 software users will call technical support.
Explanation:
Test if the normal curve can be used as an approximation to the binomial probability by verifying the necessary conditions.
It is needed that:
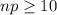 and
and
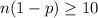
Binomial probability distribution
The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

In which
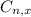 is the number of different combinations of x objects from a set of n elements, given by the following formula.
is the number of different combinations of x objects from a set of n elements, given by the following formula.
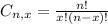
And p is the probability of X happening.
Can be approximated to a normal distribution, using the expected value and the standard deviation.
The expected value of the binomial distribution is:
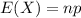
The standard deviation of the binomial distribution is:
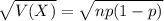
Normal probability distribution
Problems of normally distributed distributions can be solved using the z-score formula.
In a set with mean
 and standard deviation
and standard deviation
 , the z-score of a measure X is given by:
, the z-score of a measure X is given by:

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
When we are approximating a binomial distribution to a normal one, we have that
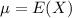 ,
,
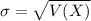 .
.
Out of 124 software users
This means that
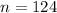
Assume the probability that a given software user will call technical support is 97%.
This means that
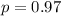
Conditions:
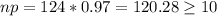
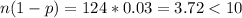
Since
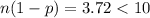 , the normal curve cannot be used as an approximation to the binomial probability.
, the normal curve cannot be used as an approximation to the binomial probability.
Consider the probability that greater than 26 out of 124 software users will call technical support.
The lowest possible probability of those is 27, so, if it is 0, since it is considerably below the mean, 100% probability of being greater. We have that:

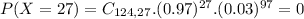
1 - 0 = 1
100% probability that greater than 26 out of 124 software users will call technical support.