A line has an equation of,
 .
.
m is called a slope
n is called y-intercept
We are also given two points
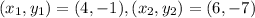 .
.
We begin with computing the slope,
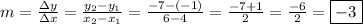
We have computed the slope m and our equation is almost done,
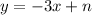
Next step is to find out what y-intercept n is. I will use point
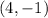 and insert x and y it into already known equation, then solve for n,
and insert x and y it into already known equation, then solve for n,
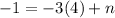
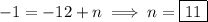
The reason I can insert coordinates of a point as x and y is because this particular point is in the line described by equation,
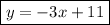
Hope this helps. :)