Answer:
The Poisson's ratio for the material is 0.0134.
Explanation:
The Poisson's ratio (
 ), no unit, is the ratio of transversal strain (
), no unit, is the ratio of transversal strain (
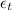 ), in inches, to axial strain (
), in inches, to axial strain (
 ), in inches:
), in inches:
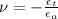 (1)
(1)
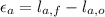 (2)
(2)
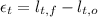 (3)
(3)
Where:
 - Initial axial length, in inches.
- Initial axial length, in inches.
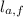 - Final axial length, in inches.
- Final axial length, in inches.
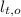 - Initial transversal length, in inches.
- Initial transversal length, in inches.
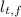 - Final transversal length, in inches.
- Final transversal length, in inches.
If we know that
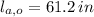 ,
,
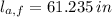 ,
,
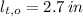 and
and
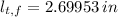 , then the Poisson's ratio is:
, then the Poisson's ratio is:
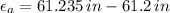
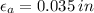
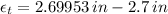
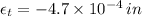
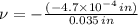

The Poisson's ratio for the material is 0.0134.