Answer:
Given that:
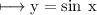
We know that,
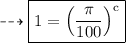
So, using this, above given can be written as,
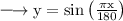
On differentiating both sides w.r.t. x, we get:
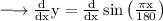
We know that,
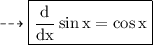
So, using the result, we get:
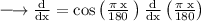
We know that,
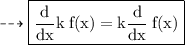
So, using this, we get:
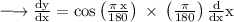
We know that,
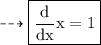
So, using this, we get:
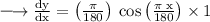
Hence:
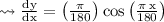
OR
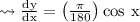

Learn More:
