Question

Find the area of the regular polygon​

Answer 1

A = 374.123 ft^2

Explanation:

First, lets calculate the perimeter:

Perimeter (p) = side length (s) * number of sides (n)

`p = s * n`

`p = 12 * 6`

`p = 72`

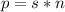
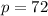
Next, lets find the apothem, which is the shortest length from any side to the middle. It's like the radius in a circle, but more complicated.

Apothem (a) = side length (s) / ( 2 * tan(180/number of sides (n)) )

`a = (s)/(2 * tan ((180)/(n) ))`

`a = (12)/(2 * tan ((180)/(6) ))`

`a = (12)/(2 * (√(3) )/(3))`

`a = (12)/((2√(3) )/(3))`

`a = (12*3)/(2√(3))`

`a = (6*3)/(√(3))`

`a = (18)/(√(3))`

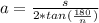
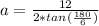
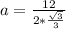
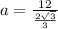
Now, finally, to find the area of a regular polygon, we use the following equation:

Area (A) = ( apothem (a) * perimeter (p) ) / 2

`A = (a * p)/(2)`

`A = ((18)/(√(3) ) * 72)/(2)`

`A = (18)/(√(3)) * 36`

`A = (640)/(√(3))`

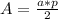
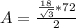
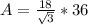
Turning into a decimal:

`A = 374.123 ft ^2`