Answer:
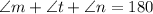
Explanation:
Required
Show that:
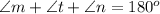
To make the proof easier, I've added a screenshot of the triangle.
We make use of alternate angles to complete the proof.
In the attached triangle, the two angles beside
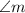 are alternate to
are alternate to
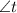 and
and
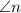
i.e.


Using angle on a straight line theorem, we have:
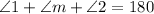
Substitute values for (1) and (2)
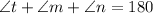
Rewrite as:
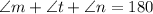 -- proved
-- proved