Question

Flying against the wind, an airplane travels 7760 kilometers in 8 hours. Flying with the wind, the same plane travels 3690 kilometers in 3 hours. What is the rate of the plane in still air and what is the rate of the wind

Answer 1

1100 and 130 (km/h)

Explanation:

1. if the velocity of the wind is 'w' and the velocity of the plane in still air is 'p', then

2. it is possible to make up two equations:

the fly against the wind: (p-w)*8=7760;

the fly with the wind: (p+w)*3=3690.

3. if to solve the system made up, then:

`\left \{ {{3(p+w)=3690} \atop {8(p-w)=7760}} \right. \ => \ \left \{ {{p+w=1230} \atop {p-w=970}} \right. \ => \ \left \{ {{p=1100} \atop {w=130}} \right.`

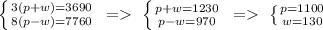
4. the required rate of the plane in still air is p=1100 km/h; the rate of the wind is w=130 km/h.