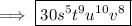Answer:
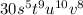
Explanation:
We'll be using the following exponent property to solve this problem:

This will allow us to combine terms with the same variable.
In
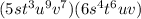 , we have four variables,
, we have four variables,
 ,
,
 ,
,
 , and
, and
 .
.
Let's start with the
 terms,
terms,
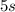 and
and
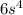 . The number in front of each term is called the coefficients, and can be multiplied directly. Remember that if there is no exponent written, it's the same thing as if there was an exponent of 1.
. The number in front of each term is called the coefficients, and can be multiplied directly. Remember that if there is no exponent written, it's the same thing as if there was an exponent of 1.
Therefore, combine using the exponent property I mentioned above:
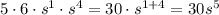
Next, we'll move on to the
 terms,
terms,
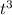 and
and
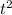 .
.
Combine using the exponent property:
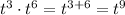
Repeat for the
 and
and
 terms:
terms:
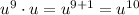
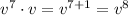
Finally, combine all the terms together: