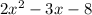Question

If fx) = 2х2 - 5 and g(x) = 3х+3, find (f-g)(x).

ОА. -Х? - 8
В. 3х - 2x2 - 2
Ос. 2х - 3x-2
OD. 2х2 – 3х – 8

Answer 1

• D:2x²-3x-8

Solution given:

f(x)=2x²-5

g(x)=3x+3

now

(f-g) (x)=?

we have

(f-g)(x)=f(x)-g(x)

• =2x²-5-(3x+3)
• =2x²-5-3x-3
• adding or subtracting common term
• =2x²-3x-8

Answer 2

`2x^(2) - 3x - 8`

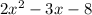
Explanation:

Step 1: Define what (f-g)(x) means

(f-g)(x) means that we have two different functions, f(x) and g(x). (f-g)(x) is a shorter way of writing f(x) - g(x). Therefore you just plug in the equations and combine like terms.

Step 2: Find (f-g)(x)

`f(x) = 2x^(2) - 5`

`g(x) = 3x + 3`

`(f-g)(x) = 2x^(2) - 5 - (3x + 3)`

`(f-g)(x) = 2x^(2) - 5 - 3x - 3`

`(f-g)(x) = 2x^(2) - 3x - 8`

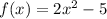
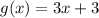
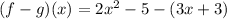
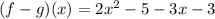
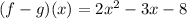
Answer:
`2x^(2) - 3x - 8`