There are two ways to go about this problem.
The first way, the generic way, is to know that,
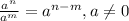 .
.
So,
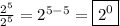 .
.
The second way is to realise that both numerator and denominator are equal and when diving two equal numbers you obtain 1. (except when diving zeros) aka,

And 1 equals to any number raised to the power of zero,
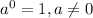
So we just have to say that the 1 we got is rewritten as some base to the power of zero.
Since our base needs to be 2, we just simply say,
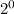 .
.
Et Viola.
Hope this helps.