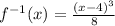Answer:
Switch x and y, and solve for y
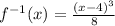
Explanation:
Given
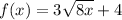
Required
Complete the steps to determine the inverse function
Solving (a): Complete the blanks
Switch x and y, and solve for y
Solving (b): Determine the inverse function
![f(x) = \sqrt[3]{8x} + 4](https://img.qammunity.org/2022/formulas/mathematics/college/rcxxbkz00vobwhwyilw2p07m2rfzbr7g2i.png)
Replace f(x) with y
![y = \sqrt[3]{8x} + 4](https://img.qammunity.org/2022/formulas/mathematics/college/n0xebwnieeyf3z606he8er8805f9p99of5.png)
Switch x and y
![x = \sqrt[3]{8y} + 4](https://img.qammunity.org/2022/formulas/mathematics/college/32g0tvrxxuc961h9o5yoj04u7r2g5gbv9c.png)
Now, we solve for y
Subtract 4 from both sides
![x -4= \sqrt[3]{8y} + 4-4](https://img.qammunity.org/2022/formulas/mathematics/college/cybicegwz3qyp6ctdtvuwtd9v4wxcf1lmv.png)
![x -4= \sqrt[3]{8y}](https://img.qammunity.org/2022/formulas/mathematics/college/o8z8zmfkorijhfuwzy1okbvtdsd2ddh1jo.png)
Take cube roots of both sides
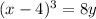
Divide both sides by 8
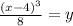
So, we have:
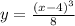
Hence, the inverse function is: