Solution :
Given information :
A sample of n = 10 adults
The mean failure was 24 and the standard deviation was 3.2
a). The formula to calculate the 95% confidence interval is given by :
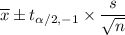
Here,
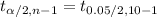
= 2.145
Substitute the values
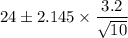
(26.17, 21.83)
When the
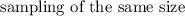 is repeated from the
is repeated from the
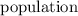
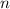 infinite number of
infinite number of
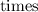 , and the
, and the
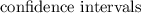 are constructed, then
are constructed, then
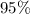 of them contains the
of them contains the
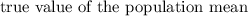 , μ in between
, μ in between
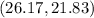
b). The formula to calculate 95% prediction interval is given by :
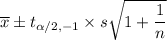
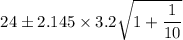
(31.13, 16.87)