Question

If a tank holds 6000 gallons of water, which drains from the bottom of the tank in 50 minutes, then Toricelli's Law gives the volume V of water remaining in the tank after t minutes as

V=5000 (1-1/50*t)^2 0⤠t ⤠50.

1. Find the rate at which water is draining from the tank after the following amount of time. (Remember that the rate must be negative because the amount of water in the tank is decreasing.)

a. 5 min
b. 10 min
c. 20 min
d. 50 min

2. At what time is the water flowing out the fastest?
3. At what time is the water flowing out the slowest?

Answer 1

Answer: hello from the question the volume of tank = 6000 gallons while the value in the Torricelli's equation = 5000 hence I resolved your question using the Torricelli's law equation

answer:

1) a) -180 gallons/minute ,

b) -160 gallons/minute

c) -120 gallons/minute

d) 0

2) The water is flowing out fastest when t = 5 min

3) The water is flowing out slowest after t = 20 mins

Explanation:

Volume of tank = 5000 gallons

Time to drain = 50 minutes

Volume of water remaining after t minutes by Torricelli's law

V = 5000 ( 1 -
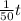`(1)/(50)t` )^2 ----- ( 1 )

1) Determine the rate at which water is draining from the tank

First step : differentiate equation 1 using the chain rule to determine the rate at which water is draining from the tank

V' =
`-10000[ ( 1 - (1)/(50)t ) ((1)/(50)) ]`

a) After t = 5minutes

V' = - 10000[ ( 1 - 0.1 ) * ( 0.02 ) ]

= -180 gallons/minute

b) After t = 10 minutes

V' = - 10000[ ( 1 - 0.2 ) * ( 0.02 ) ]

= - 160 gallons/minute

c) After t = 20 minutes

V' = - 10000 [ ( 1 - 0.4 ) * ( 0.02 ) ]

= -120 gallons/minute

d) After t = 50 minutes

V' = - 10000 [ ( 1 - 1 ) * ( 0.02 ) ]

= 0 gallons/minute

2) The water is flowing out fastest when t = 5 min

3) The water is flowing out slowest after t = 20 mins because no water flows out after 50 minutes