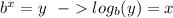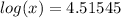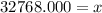Question

If log2 X + log4 X = 5, find X for the 3 decimal places.

Answer 1

`x=32768.000`

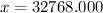
Explanation:

One is given the following expression:

`log_2(x)+log_4(x)=5`

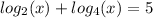
Use the logarithm base change rule, which states the following:

`log_b(y)=(log(y))/(log(b))`

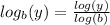
Remember, a logarithm with not base indicated is another way of writing a logarithm to the base of (10). One can apply the base change rule to this situation:

`log_2(x)+log_4(x)=5`

`(log(x))/(log(2))+(log(x))/(log(4))=5`

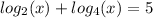
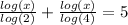
Factor out (log(x)),

`(log(x))((1)/(log(2))+(1)/(log(4)))=5`

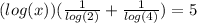
Inverse operations:

`log(x)=(5)/((1)/((log(2)+log(4)))`

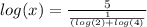
Simplify,

`log(x)=5(log(2)+log(4))`

`log(x)=4.51545`

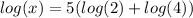
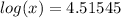
Now rewrite the logarithm, remember, a logarithm is another way of writing an exponent, in the following format:

`b^x=y\ \ -> log_b(y)=x`

`log(x)=4.51545`

`10^4^.^5^1^5^4^5=x`

`32768.000=x`