Question

What else would need to be congruent to show that ABC= A DEF by the

AAS theorem?
B
E
Given:
ZA ZD
AB DE
A
F
A. AC = DF
B. ZCE ZF
C. BC = BC
D. BEZE

Answer 1

`\angle C \cong \angle F`

Explanation:

Given

`\angle A \cong \angle D`

`AB \cong DE`

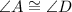
See attachment

Required

What proves
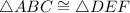`\triangle ABC \cong \triangle DE F` by AAS

We have:

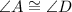`\angle A \cong \angle D` --- Angle

`AB \cong DE` --- Side

We need to prove that one more angle are congruent

`\angle B \cong \angle E`

The above angles are congruent; however, it will prove
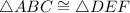`\triangle ABC \cong \triangle DE F` by ASA

So, we make use of:

`\angle C \cong \angle F` because it completes the proof by AAS