Question

Which graph represents the function f (x) = StartFraction 2 Over x minus 1 EndFraction + 4?

On a coordinate plane, a hyperbola is shown. One curve opens up and to the right in quadrant 1, and the other curve opens down and to the left in quadrant 3. A vertical asymptote is at x = 1, and the horizontal asymptote is at y = negative 4.
On a coordinate plane, a hyperbola is shown. One curve opens up and to the right in quadrant 1, and the other curve opens down and to the left in quadrant 3. A vertical asymptote is at x = negative 1, and the horizontal asymptote is at y = negative 4.
On a coordinate plane, a hyperbola is shown. One curve opens up and to the right in quadrant 1, and the other curve opens down and to the left in quadrant 3. A vertical asymptote is at x = negative 1, and the horizontal asymptote is at y = 4.
On a coordinate plane, a hyperbola is shown. One curve opens up and to the right in quadrant 1, and the other curve opens down and to the left in quadrant 3. A vertical asymptote is at x = 1, and the horizontal asymptote is at y = 4.

Answer 1

On a coordinate plane, a hyperbola is shown. One curve opens up and to the right in quadrant 1, and the other curve opens down and to the left in quadrant 3. A vertical asymptote is at x = 1, and the horizontal asymptote is at y = 4

Explanation:

The given function is presented as follows;

`f(x) = (2)/(x - 1) + 4`

From the given function, we have;

When x = 1, the denominator of the fraction,
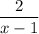`(2)/(x - 1)`, which is (x - 1) = 0, and the function becomes,
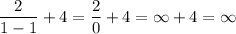`(2)/(1 - 1) + 4 = (2)/(0) + 4 = \infty + 4 = \infty` therefore, the function in undefined at x = 1, and the line x = 1 is a vertical asymptote

Also we have that in the given function, as x increases, the fraction
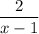`(2)/(x - 1)` tends to 0, therefore as x increases, we have;

`\lim_ {x \to \infty} (2)/((x - 1)) \to 0, and \ (2)/((x - 1)) + 4 \to 4`

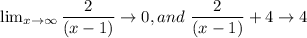
Therefore, as x increases, f(x) → 4, and 4 is a horizontal asymptote of the function, forming a curve that opens up and to the right in quadrant 1

When -∞ < x < 1, we also have that as x becomes more negative, f(x) → 4. When x = 0,
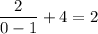`(2)/(0 - 1) + 4 = 2`. When x approaches 1 from the left, f(x) tends to -∞, forming a curve that opens down and to the left

Therefore, the correct option is on a coordinate plane, a hyperbola is shown. One curve opens up and to the right in quadrant 1, and the other curve opens down and to the left in quadrant 3. A vertical asymptote is at x = 1, and the horizontal asymptote is at y = 4.