Question

A monatomic gas is measured to have an average speed of 1477 m/s. If the

total amount of the gas is 2 mol (which equates to a mass of 0.008 kg), what
is the approximate temperature of the gas? (Recall that the equation for
kinetic energy due to translation in a gas is KEtranslational = 1 mv2 = 3 nRT,
2
and R = 8.31 J/(mol-K).)
2

Answer 1

The temperature of the gas is 350.02 K.

Step-by-step explanation:

The average speed is related to the temperature as follows:

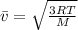`\bar v = \sqrt{(3RT)/(M)}` (1)

Where:

`\bar v`: is the average speed = 1477 m/s

R: is the gas constant = 8.31 J/(K*mol)

T. is the temperature =?

M: is the molar mass

First, let's find the molar mass:

`M = (m)/(n)`

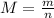
Where:

m: is the mass of the gas = 0.008 kg

n: is the number of moles = 2 mol

`M = (m)/(n) = (0.008 kg)/(2 mol) = 0.004 kg/mol`

Hence, by solving equation (1) fot T we have:

`T = (\bar v^(2)*M)/(3R) = ((1477 m/s)^(2)*0.004 kg/mol)/(3*8.31 J/(K*mol)) = 350.02 K`

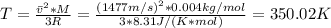
Therefore, the temperature of the gas is 350.02 K.

I hope it helps you!