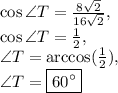Answer:
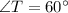
Explanation:
In all 30-60-90 triangles, the sides are in ratio
 , where
, where
 is the side opposite to the 30 degree angle and
is the side opposite to the 30 degree angle and
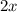 is the hypotenuse of the triangle. We know that two right triangles are created on both sides of the rectangle in the center. Notice that
is the hypotenuse of the triangle. We know that two right triangles are created on both sides of the rectangle in the center. Notice that
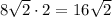 and since
and since
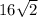 is the hypotenuse of the right triangle on the left,
is the hypotenuse of the right triangle on the left,
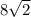 must be facing the 30 degree angle. Therefore, angle T must be 60 degrees.
must be facing the 30 degree angle. Therefore, angle T must be 60 degrees.
Alternatively, the cosine of any angle in a right triangle is equal to its adjacent side divided by the hypotenuse.
Therefore, we have: