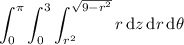Question

Change to cylindrical coordinates. 3∫−3 9-x^2∫0 9−x^2-y^2∫x^2+y^2 dz dy dx

Answer 1

I think the given integral reads

`\displaystyle \int_(-3)^3 \int_0^(9-x^2) \int_(x^2+y^2)^(9-x^2-y^2) \mathrm dz\,\mathrm dy\,\mathrm dx`

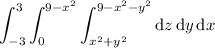
In cylindrical coordinates, we take

x ² + y ² = r ²

x = r cos(θ)

y = r sin(θ)

and leave z alone. The volume element becomes

dV = dx dy dz = r dr dθ dz

Then the integral in cylindrical coordinates is

`\displaystyle \boxed{\int_0^\pi \int_0^((√(35\cos^2(\theta)+1)-\sin(\theta))/(2\cos^2(\theta))) \int_(r^2)^(9-r^2) r\,\mathrm dz\,\mathrm dr\,\mathrm d\theta}`

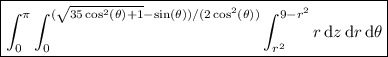
To arrive at this integral, first look at the "shadow" of the integration region in the x-y plane. It's the set

{(x, y) : -3 ≤ x ≤ 3 and 0 ≤ y ≤ 9 - x ²}

which is the area between a paraboloid and the x-axis in the upper half of the plane. So right away, you know θ will fall in the first two quadrants, so that 0 ≤ θ ≤ π.

Next, r describes the distance from the origin to the parabola y = 9 - x ². In cylindrical coordinates, this equation changes to

r sin(θ) = 9 - (r cos(θ))²

You can solve this explicitly for r as a function of θ :

r sin(θ) = 9 - r ² cos²(θ)

r ² cos²(θ) + r sin(θ) = 9

r ² + r sin(θ)/cos²(θ) = 9/cos²(θ)

(r + sin(θ)/(2 cos²(θ)))² = 9/cos²(θ) + sin²(θ)/(4 cos⁴(θ))

(r + sin(θ)/(2 cos²(θ)))² = (36 cos²(θ) + sin²(θ))/(4 cos⁴(θ))

(r + sin(θ)/(2 cos²(θ)))² = (35 cos²(θ) + 1)/(4 cos⁴(θ))

r + sin(θ)/(2 cos²(θ)) = √[(35 cos²(θ) + 1)/(4 cos⁴(θ))]

r = √[(35 cos²(θ) + 1)/(4 cos⁴(θ))] - sin(θ)/(2 cos²(θ))

Then r ranges from 0 to this upper limit.

Lastly, the limits for z can be converted immediately since there's no underlying dependence on r or θ.

The expression above is a bit complicated, so I wonder if you are missing some square roots in the given integral... Perhaps you meant

`\displaystyle \int_(-3)^3 \int_0^(√(9-x^2)) \int_(x^2+y^2)^(9-x^2-y^2) \mathrm dz\,\mathrm dy\,\mathrm dx`

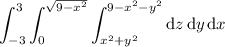
or

`\displaystyle \int_(-3)^3 \int_0^(√(9-x^2)) \int_(x^2+y^2)^(√(9-x^2-y^2)) \mathrm dz\,\mathrm dy\,\mathrm dx`

For either of these, the "shadow" in the x-y plane is a semicircle of radius 3, so the only difference is that the upper limit on r in either integral would be r = 3. The limits for z would essentially stay the same. So you'd have either

`\displaystyle \int_0^\pi \int_0^3 \int_(r^2)^(9-r^2) r\,\mathrm dz\,\mathrm dr\,\mathrm d\theta`

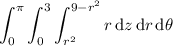
or

`\displaystyle \int_0^\pi \int_0^3 \int_(r^2)^(√(9-r^2)) r\,\mathrm dz\,\mathrm dr\,\mathrm d\theta`