Answer:
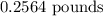
Explanation:
The 90th percentile of a normally distributed curve occurs at 1.282 standard deviations. Similarly, the 10th percentile of a normally distributed curve occurs at -1.282 standard deviations.
To find the
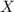 percentile for the television weights, use the formula:
percentile for the television weights, use the formula:
 , where
, where
 is the average of the set,
is the average of the set,
 is some constant relevant to the percentile you're finding, and
is some constant relevant to the percentile you're finding, and
 is one standard deviation.
is one standard deviation.
As I mentioned previously, 90th percentile occurs at 1.282 standard deviations. The average of the set and one standard deviation is already given. Substitute
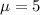 ,
,
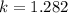 , and
, and
 :
:
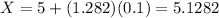
Therefore, the 90th percentile weight is 5.1282 pounds.
Repeat the process for calculating the 10th percentile weight:
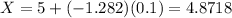
The difference between these two weights is
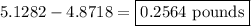 .
.