Question

Given $f(x) = \frac{\sqrt{2x-6}}{x-3}$, what is the smallest possible integer value for $x$ such that $f(x)$ has a real number value? Please show steps. Thank you!

(I rewrote the question without the symbols, they are the same question)

Given f(x) = {2x-6}/{x-3}, what is the smallest possible integer value for x such that f(x) has a real number value? Thank you!​

Answer 1

Answer: x = 4

===========================================================

Step-by-step explanation:

The given function is

`f(x) = (√(2x-6))/(x-3)`

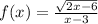
which is the same as writing f(x) = ( sqrt(2x-6) )/(x-3)

The key for now is the square root term. Specifically, the stuff underneath. This stuff is called the radicand.

Recall that the radicand cannot be negative, or else the square root stuff will result in a complex number. Eg:
`√(-4) = 0+2i`

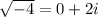
The question is basically asking: what is the smallest x such that
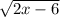`√(2x-6)` is a real number?

Well if we made 2x-6 as small as possible, ie set it equal to 0, then we can find the answer

`2x-6 = 0\\\\2x = 6\\\\x = 6/2\\\\x = 3\\\\`

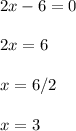
I set the radicand equal to 0 because that's as small as the radicand can get (otherwise, we're dipping into negative territory).

So 2x-6 set equal to 0 leads to x = 3.

This means x = 3 produces the smallest radicand (zero) and therefore, it is the smallest allowed x value for that square root term.

But wait, if we tried x = 3 in f(x), then we get...

`f(x) = (√(2x-6))/(x-3)\\\\f(3) = (√(2*3-6))/(3-3)\\\\f(3) = (√(0))/(0)\\\\`

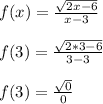
which isn't good. We cannot have 0 in the denominator. Dividing by zero is not allowed. The result is undefined. It doesn't even lead to a complex number. So we'll need to bump x = 3 up to x = 4. You should find that x = 4 doesn't make the denominator 0.

----------------

In short, we found that x = 3 makes the square root as small as possible while staying a real number, but it causes a division by zero error with f(x) overall. So we bump up to x = 4 instead.