Answer:
x = 12
perimeter = 113 units
Explanation:
Triangle Proportionality Theorem states that if a line parallel to one side of the triangle intersects the other two sides, then it divides the sides into proportional corresponding segments.
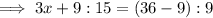
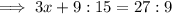
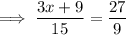
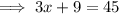
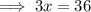
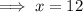
Perimeter =
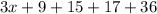
Substituting
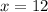 :
:
⇒ perimeter = 3(12) + 9 + 15 + 17 + 36
= 113