Answer:

Step-by-step explanation:
Hello there!
In this case, according to the given information, it turns out firstly necessary for us to set up the van der Waals' equation as shown below:
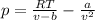
Thus, we secondly calculate the molar volume as:

Then, we plug in the entire variables in the vdW equation to get such pressure:
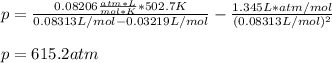
And the ideal gas pressure:
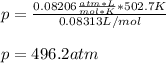
Finally, the percent difference:
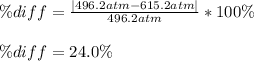
Regards!