Part A:
What is the maximum height the ball will reach in the air?
Kinematics equation used:
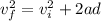 , where
, where
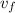 is final velocity,
is final velocity,
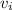 is initial velocity,
is initial velocity,
 is acceleration, and
is acceleration, and
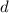 is distance travelled. From SI units, velocity should be in
is distance travelled. From SI units, velocity should be in
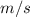 , acceleration should be in
, acceleration should be in
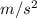 , and distance should be in
, and distance should be in
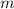
We're given that the initial velocity is 12.0 m/s in the y-direction. At the maximum height, the vertical velocity of the ball will be 0 m/s, otherwise it would not be at maximum height. This is our final velocity.
The only acceleration in the system is acceleration due to gravity, which is approximately
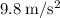 . However, the acceleration is acting down, whereas the ball is moving up. To express its direction, acceleration should be plugged in as
. However, the acceleration is acting down, whereas the ball is moving up. To express its direction, acceleration should be plugged in as
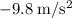 . We have three variables, and we are solving for the fourth, which is distance travelled. This will be the maximum height of the ball.
. We have three variables, and we are solving for the fourth, which is distance travelled. This will be the maximum height of the ball.
Substitute
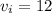 ,
,
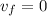 ,
,
 to solve for
to solve for
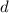 :
:
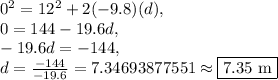
What is the velocity of the ball when it hits the ground?
This question tests a physics concept rather than a physics formula. The vertical velocity of the ball when it hits the ground is equal in magnitude but opposite in direction to the ball's initial vertical velocity. This is because the ball spends equal time travelling to its max height as it does travelling from max height to the ground (ball is accelerating from initial velocity to 0 and then from 0 to some velocity over the same distance and time). Since the ball has an initial vertical velocity of +12.0 m/s, its velocity when it hits the ground will be
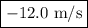 . (The negative sign represents the direction. Because velocity is a vector, it is required.)
. (The negative sign represents the direction. Because velocity is a vector, it is required.)
Part B:
**Since my initial answer exceeds the character limit, I've attached the first question to Part B as an image. Please refer to the attached image for the answer and explanation to the first question of Part B. Apologies for the inconvenience.**
What is the direction of the velocity of the ball when it hits the ground? Express your answer in terms of the angle (in degrees ) of the ball's velocity with respect to the horizontal direction (see figure).
This question uses a similar concept as the second question of Part A. The vertical velocity of the ball at launch is equal in magnitude but opposite in direction to the ball's final velocity. The horizontal component is equal in both magnitude and direction throughout the entire launch, since there are no horizontal forces acting on the system. Therefore, the angle below the horizontal of the ball's velocity when it hits the ground is equal to the angle of the ball to the horizontal at launch.
To find this, we need to use basic trigonometry for a right triangle. In any right triangle, the tangent/tan of an angle is equal to its opposite side divided by its adjacent side.
Let the angle to the horizontal at launch be
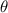 . The angle's opposite side is represented by the vertical velocity at launch (12.0 m/s) and the angle's adjacent side is represented by the horizontal velocity at launch (2.3 m/s). Therefore, we have the following equation:
. The angle's opposite side is represented by the vertical velocity at launch (12.0 m/s) and the angle's adjacent side is represented by the horizontal velocity at launch (2.3 m/s). Therefore, we have the following equation:
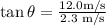
Take the inverse tangent of both sides:
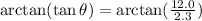
Simplify using
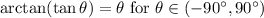 :
:
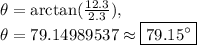
We can express our answer by saying that the direction of the velocity of the ball when it hits the ground is
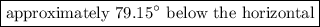 or
or
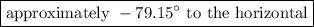 .
.