Answer:
To obtain a "B", Rita needs to score between 76.7 and 100.
Explanation:
Chapter tests mean:
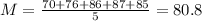
Grades:
80.8 worth 60% = 0.6
85 worth 10% = 0.1
x worth 0.3.
So her grade is:
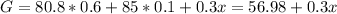
What scores can Rita earn on the final exam to earn a "B" in the course if the cut-off for a "B" is an overall score greater than or equal to 80, but less than 90?
G has to be greater than or equal to 80 and less than 90, so:
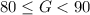
Lower bound:

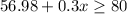
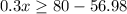
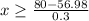
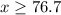
Upper bound:
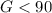

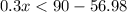
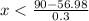
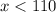
Highest grade is 100, so:
To obtain a "B", Rita needs to score between 76.7 and 100.