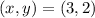Create a system of linear equations with one solution. In your final answer, include the system of equations and the graphs of the lines.

Question

asked May 11, 2022 180k views

1 Answer

Rohit Karadkar · Answer 1 · 2022-05-15T22:05:30+0000

Answer:

System of equations

x + y = 5

y - 2x = -4

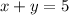
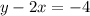
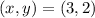(x,y) = (3,2) --- solution

See attachment for graph

Explanation:

Solving (a): Linear equations with 1 solution

The only condition to this is that, the system must have 1 solution.

Other than that, there is no other condition.

A linear equation is represented as:

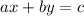
ax + by= c

For the equation to have 1 solution;

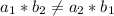
$a_1 * b_2 \\e a_2 * b_1$

And example of such equation is:

x + y = 5

y - 2x = -4

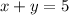
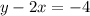
Solving (b): The graph

See attachment for graph

The solution is the point of intersection of both lines of the graph. So, we have:

(x,y) = (3,2)