Answer:
A) x = 0.
B) f is concave up for (-∞, 0).
C) f is concave down for (0, ∞).
Explanation:
We are given the function:
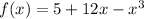
A)
We want to find the x-coordinates of all inflection points.
Recall that inflections points (may) occur when the second derivative equals zero. Hence, find the second derivative. The first derivative is given by:
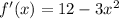
And the second:
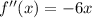
Set the second derivative equal to zero:

And solve for x. Hence:
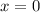
We must test the solution. In order for it to be an inflection point, the second derivative must change signs before and after. Testing x = -1:
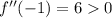
And testing x = 1:

Since the signs change for x = 0, x = 0 is indeed an inflection point.
B)
Recall that f is concave up when f''(x) is positive, and f is concave down when f''(x) is negative.
From the testing in Part A, we know that f''(x) is positive for all values less than zero. Hence, f is concave up for all values less than zero. Our interval is:
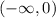
C)
From Part A, we know that f''(x) is negative for all values greater than zero. So, f is concave down for that interval:
