Answer:
Approximately
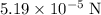 .
.
Step-by-step explanation:
Let
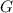 denote the gravitational constant. (
denote the gravitational constant. (
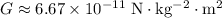 .)
.)
Let
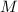 and
and
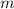 denote the mass of two objects separated by
denote the mass of two objects separated by
 .
.
By Newton's Law of Universal Gravitation, the gravitational attraction between these two objects would measure:
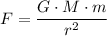 .
.
In this question:
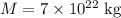 is the mass of the moon, while
is the mass of the moon, while
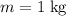 is the mass of the water. The two are
is the mass of the water. The two are
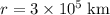 apart from one another.
apart from one another.
Important: convert the unit of
 to standard units (meters, not kilometers) to reflect the unit of the gravitational constant
to standard units (meters, not kilometers) to reflect the unit of the gravitational constant
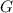 .
.
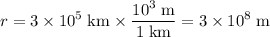 .
.
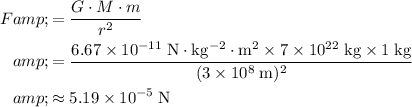 .
.