Start with the answer format we want, and work your way toward forming a single fraction like so
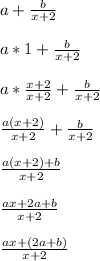
Compare that last expression to (2x+1)/(x+2). Notice how the ax and 2x match up, so a = 2 must be the case.
Then we have 2a+b as the remaining portion in the numerator. Plugging in a = 2 leads to 2a+b = 2*2+b = 4+b. Set this equal to the +1 found in (2x+1)/(x+2) to have the terms match.
So, 4+b = 1 leads to b = -3
Therefore, a = 2 and b = -3
------------------------------------------------
An alternative route:
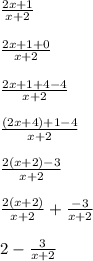
I added and subtracted 4 in the third step so that I could form 2x+4, which then factors to 2(x+2). That way I could cancel out a pair of (x+2) terms toward the very end.
------------------------------------------------
Other alternative methods involve synthetic division or polynomial long division. They are slightly separate but related concepts.