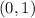Answer:
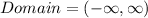
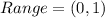
Explanation:
Given
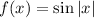
Solving (a): The domain
There is no restriction on the given function because it is not a root function and doesn't have a x denominated fraction
Hence, the domain is:
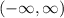
Solving (b): The range
The minimum of a sine function is 0
The maximum of a sine function is 1
So, the range is: