Question

The restrictions for f(x)=2x+3/x^2−4 are ±2


True

False

Answer 1

Answer: True

=========================================================

Step-by-step explanation:

If you meant to say
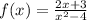`f(x) = (2x+3)/(x^2-4)`, then we cannot have x^2-4 equal to 0

We can never have 0 in the denominator.

Set the expression equal to 0 and solve for x

x^2 - 4 = 0

(x-2)(x+2) = 0 .... difference of squares rule

x-2 = 0 or x+2 = 0

x = 2 or x = -2

So if either x = 2 or x = -2, then we have x^2-4 equal to zero.

So these are the values we must kick out of the domain to avoid a division by zero error.

In short, the restrictions for x are 2 and -2. That's why the statement is true.