Given:
The function are:
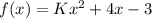
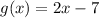
The graph of f(x) intersect the line g(x) at one point.
To find:
The value of K.
Solution:
The graph of f(x) intersect the line g(x) at one point. It means the line g(x) is the tangent line.
We have,
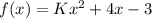
Differentiate this function with respect to x.
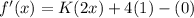
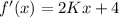
Let the point of tangency is
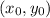 . So, the slope of the tangent line is:
. So, the slope of the tangent line is:
![[f'(x)]_((x_0,y_0))=2Kx_0+4](https://img.qammunity.org/2022/formulas/mathematics/high-school/umh323vq02eotidn9rlyb3re18lejuof4g.png)
On comparing
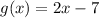 with slope-intercept form, we get
with slope-intercept form, we get
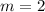
So, the slope of the tangent line is 2.
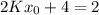
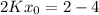
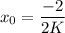
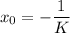
Putting
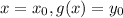 in g(x), we get
in g(x), we get
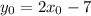
Putting
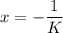 in the above equation, we get
in the above equation, we get
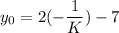
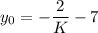
Putting
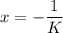 and
and
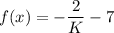 in f(x).
in f(x).
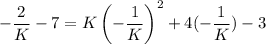
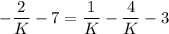
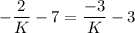
Multiply both sides by K.
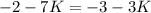
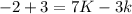
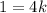
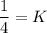
Therefore, the value of K is
 .
.