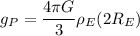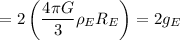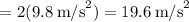Step-by-step explanation:
The density of earth
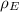 is given by
is given by
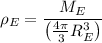
and in terms of this density, we can write the acceleration due to gravity on earth as
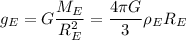
Similarly, the acceleration due to gravity
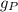 on this new planet is given by
on this new planet is given by
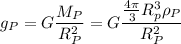
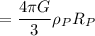
We know that this planet has the same density as earth and has a radius 2 times as large. We can then rewrite
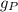 as
as