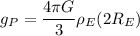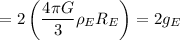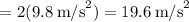Question

In December of 2011 they announced that a planet has been discovered in a habitable zone around a

star! It has clouds! It has twice the radius of the earth, but with the same density as earth, about 5.515 × 10^3kg/m3
. Find the new acceleration of gravity on the surface of this planet.

Answer 1

Step-by-step explanation:

The density of earth
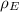`\rho_E` is given by

`\rho_E = (M_E)/(\left((4\pi)/(3)R_E^3\right))`

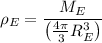
and in terms of this density, we can write the acceleration due to gravity on earth as

`g_E =G(M_E)/(R_E^2) = (4\pi G)/(3)\rho_ER_E`

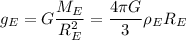
Similarly, the acceleration due to gravity
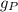`g_P` on this new planet is given by

`g_P = G(M_P)/(R_P^2) = G((4\pi)/(3)R_p^3\rho_P)/(R_P^2)`

`\:\:\:\:\:= (4\pi G)/(3)\rho_PR_P`

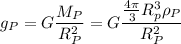
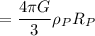
We know that this planet has the same density as earth and has a radius 2 times as large. We can then rewrite
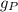`g_P` as

`g_P = (4\pi G)/(3)\rho_E(2R_E)`

`\:\:\:\:\:= 2\left((4\pi G)/(3)\rho_ER_E\right) = 2g_E`

`\:\:\:\:\:= 2(9.8\:\text{m/s}^2) = 19.6\:\text{m/s}^2`