Question

Calculate the number of hydrogen atoms in 33.0 g CH4

Answer 1

The number of hydrogen atoms is 4.96x10²⁴.

Step-by-step explanation:

The number of atoms can be found with the following equation:

`n = N*\eta_(H)`

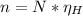
Where:

N: is the Avogadro's number = 6.022x10²³ atoms/mol

η: is the number of moles of hydrogen

n: is the number of hydrogen atoms

First, we need to find the number of hydrogen moles. The number of moles of CH₄ is:

`\eta_{CH_(4)} = (m)/(M)`

Where:

m: is the mass of methane = 33 g

M: is the molar mass of methane = 16.04 g/mol

`\eta_{CH_(4)} = (33 g)/(16.04 g/mol) = 2.06 mol`

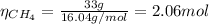
Now, since we have 4 hydrogen atoms in 1 mol of methane, the number of moles of hydrogen is:

`\eta_(H) = 2.06\: mol\: CH_(4)*4 (mol\: H)/(mol \: CH_(4)) = 8.24 mol`

Hence, the number of hydrogen atoms is:

`n = N*\eta_(H) = 6.022 \cdot 10^(23) \: atoms/mol*8.24 mol = 4.96 \cdot 10^(24) atoms`

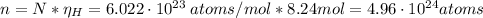
Therefore, the number of hydrogen atoms is 4.96x10²⁴.

I hope it helps you!