Question

If a conducting loop of radius 10 cm is onboard an instrument on Jupiter at 45 degree latitude, and is rotating with a frequency 2 rev/s; What is the maximum emf induced in this loop? If its resistance is 0.00336 ohms, how much current is induced in this loop? And what is the maximum power dissipated in the loop due to its rotation in Jupiter's magnetic field?

Answer 1

a) fem = - 2.1514 10⁻⁴ V, b) I = - 64.0 10⁻³ A, c) P = 1.38 10⁻⁶ W

Step-by-step explanation:

This exercise is about Faraday's law

fem =
`- ( d \Phi_B)/(dt)`

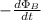
where the magnetic flux is

Ф = B x A

the bold are vectors

A = π r²

we assume that the angle between the magnetic field and the normal to the area is zero

fem = - B π 2r dr/dt = - 2π B r v

linear and angular velocity are related

v = w r

w = 2π f

v = 2π f r

we substitute

fem = - 2π B r (2π f r)

fem = -4π² B f r²

For the magnetic field of Jupiter we use the equatorial field B = 428 10⁻⁶T

we reduce the magnitudes to the SI system

f = 2 rev / s (2π rad / 1 rev) = 4π Hz

we calculate

fem = - 4π² 428 10⁻⁶ 4π 0.10²

fem = - 16π³ 428 10⁻⁶ 0.010

fem = - 2.1514 10⁻⁴ V

for the current let's use Ohm's law

V = I R

I = V / R

I = -2.1514 10⁻⁴ / 0.00336

I = - 64.0 10⁻³ A

Electric power is

P = V I

P = 2.1514 10⁻⁴ 64.0 10⁻³

P = 1.38 10⁻⁶ W