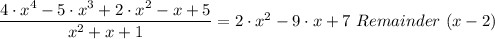Answer:
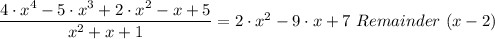
Explanation:
Part I
The problem can be expressed as follows;
The dividend is 4·x⁴ - 5·x³ + 2·x² - x + 5
The divisor is x² + x + 1
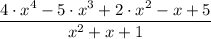
Part II
The number of times x² goes into the larest term, 4·x⁴ = 4·x² times
2·x² - 9·x + 7
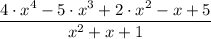
4·x⁴ + 4·x³ + 4·x²
-9·x³ - 2·x² - x + 5
-9·x³ - 9·x² - 9·x
7·x² + 8·x + 5
7·x² + 7·x + 7
x - 2
Therefore, we have;