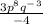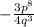Answer:
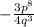
Explanation:
One is given the following expression,
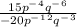
Since (15) and (-20) are both divisible by (5), one can divide both terms by (5) to simplify it.
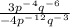
Now bring all of the terms with a negative exponent to the numerator. Multiply the exponents by (-1), then add them to the exponents of the like term in the numerator. Simplify the resulting exponents
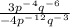
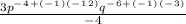
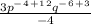
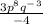
Rewrite the fraction such that there are no negative exponents. Remember the rule, when bringing a number from the numerator to the denominator and back, multiply the exponent of the number by (-1). One can only switch numbers between the numerator and the denominator when all operations are multiplication or division.