Question

Howard invested $5,000 in Certificate of Deposit (CD) that pays 3.75% interest. compounded weekly. What is the value of the CD at the end of the 4 years?

Answer 1

The value of the CD at the end of the 4 years is $5,808.86.

Explanation:

Compound interest:

The compound interest formula is given by:

`A(t) = P(1 + (r)/(n))^(nt)`

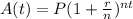
Where A(t) is the amount of money after t years, P is the principal(the initial sum of money), r is the interest rate(as a decimal value), n is the number of times that interest is compounded per year and t is the time in years for which the money is invested or borrowed.

Howard invested $5,000 in Certificate of Deposit (CD) that pays 3.75% interest.

This means that
`P = 5000, r = 0.0375`

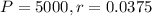
Compounded weekly

An year has 52 weeks, so
`n = 52`

Then

`A(t) = P(1 + (r)/(n))^(nt)`

`A(t) = 5000(1 + (0.0375)/(52))^(52t)`

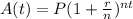
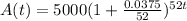
What is the value of the CD at the end of the 4 years?

This is A(4). So

`A(4) = 5000(1 + (0.0375)/(52))^(52*4) = 5808.86`

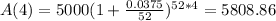
The value of the CD at the end of the 4 years is $5,808.86.