Question

Categorize the trigonometric functions as positive or negative.

Answer 1

So, remember that:

cos(x) > 0 for -pi/2 < x < pi/2

cos(x) < 0 for pi/2 < x < (3/2)*pi

and

sin(x) > 0 for 0 < x < pi

sin(x) < 0 for -pi < x <0 or pi < x < 2pi

Also, we have the periodicty of the sine and cocine equations, such that:

sin(x) = sin(x + 2pi)

cos(x) = cos(x + 2pi)

Now let's solve the problem:

`sin((13*\pi)/(36) )`

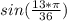
here we have:

x = (13/36)π

This is larger than zero and smaller than π:

0 < (13/36)π < π

then:

`sin((13*\pi)/(36) )`

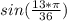
Is positive.

The next one is:

`cos((7*\pi)/(12) )`

Here we have x = (7/12)*pi

notice that:

7/12 > 1/2

Then:

(7/12)*π > (1/2)*π

Then:

`cos((7*\pi)/(12) )`

is negative.

next one:

`sin((47*\pi)/(36) )`

here:

x = (47/36)*π

here we have (47/36) > 1

then:

(47/36)*π > π

then:

`sin((47*\pi)/(36) )`

is negative.

the next one is:

`cos((17*\pi)/(10) )`

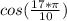
Here we have x = (17/10)*π

if we subtract 2*π (because of the periodicity) we get:

(17/10)*π - 2*π

(17/10)*π - (20/10)*π

(-3/10)*π

this is in the range where the cosine function is positive, thus:

`cos((17*\pi)/(10) )`

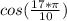
is positive.

the next one is:

`tan((41*\pi)/(36) ) = (sin((41*\pi)/(36) ))/(cos((41*\pi)/(36) ))`

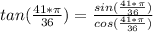
here we have:

x = (41/36)*π

Notice that both functions, sine and cosine are negatives for that value, then we have the quotient of two negative values, so:

`tan((41*\pi)/(36) ) = (sin((41*\pi)/(36) ))/(cos((41*\pi)/(36) ))`

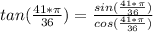
is positive.

The final one is:

`tan((5*\pi)/(9) ) = (sin((5*\pi)/(9) ))/(cos((5*\pi)/(9) ))`

Here:

x = (5/9)*π

The sin function is positive with this x value, while the cosine function is negative, thus:

`tan((5*\pi)/(9) ) = (sin((5*\pi)/(9) ))/(cos((5*\pi)/(9) ))`

Is negative.