Answer:
Explanation:
The easiest way to do this is to complete the square on the quadratic. This allows us to see what the vertex is and answer the question without having to plug in a ton of numbers to see what the max y value is. Completing the square will naturally put the equation into vertex form:
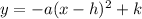 where h will be the time it takes to get to a height of k.
where h will be the time it takes to get to a height of k.
Begin by setting the quadratic equal to 0 and then moving over the constant, like this:
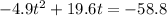 and the rule is that the leading coefficient has to be a 1. Ours is a -4.9 so we have to factor it out:
and the rule is that the leading coefficient has to be a 1. Ours is a -4.9 so we have to factor it out:
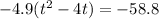 Now take half the linear term, square it, and add it to both sides. Our linear term is a -4, from -4t. Half of -4 is -2, and -2 squared is 4, so we add a 4 to both sides. BUT on the left we have that -4.9 out front there as a multiplier, so we ACTUALLY added on to the left was -4.9(4) which is -19.6:
Now take half the linear term, square it, and add it to both sides. Our linear term is a -4, from -4t. Half of -4 is -2, and -2 squared is 4, so we add a 4 to both sides. BUT on the left we have that -4.9 out front there as a multiplier, so we ACTUALLY added on to the left was -4.9(4) which is -19.6:
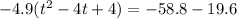 and now we have to clean this up. The right side is easy, that is -78.4. The left side...not so much.
and now we have to clean this up. The right side is easy, that is -78.4. The left side...not so much.
The reason we complete the square is to create a perfect square binomial, which is the
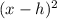 part from above. Completing the square does this naturally, now it's just up to us to write the binomial created during the process:
part from above. Completing the square does this naturally, now it's just up to us to write the binomial created during the process:
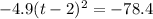 Now, move the constant back over and set the equation back equal to y:
Now, move the constant back over and set the equation back equal to y:
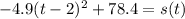 and we see that the vertex is (2, 78.4). That means that 2 seconds after launch, the object reached its max height of 78.4 meters, the third choice down.
and we see that the vertex is (2, 78.4). That means that 2 seconds after launch, the object reached its max height of 78.4 meters, the third choice down.