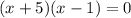Question

What equation reoulte from completing the square and then factoring?
x2 + 4x-5

Answer 1

Completing the square:
`(x^2+4x)-5=0`

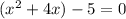
Factored form:
`(x+5)(x-1)=0`

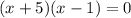
Explanation:

1.

Completing the square is a method used to rewrite a quadratic equation in vertex form. First one groups the linear and the quadratic terms. Then one will factor out the coefficient of the quadratic term. After doing so, one makes the grouped equation a perfect square trinomial by introducing a term, don't forget to balance the equation. Finally one simplifies the equation. The result is a quadratic equation in vertex form.

The quadratic equation:

`x^2+4x-5=0`

Group the linear and quadratic terms:

`(x^2+4x)-5=0`

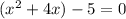
The quadratic term doesn't have a coefficient, so one doesn't need to factor the group. Now, one has to add a term to make the group a perfect square trinomial. Remember to balance the equation:

`(x^4+4x-4)-5-4=0`

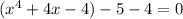
Simplify,

`(x-2)^2-9=0`

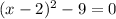
2.

Factoring a quadratic equation is a method of rewriting a quadratic equation as the product of two linear equations. One splits the constant term up into factors, such that the sum of the factors is equal to the coefficient of the linear term.

`x^2+4x-5=0`

Factor:

`(x+5)(x-1)=0`