Answer:
Explanation:
We are looking for P(58 < x < 64). We need to find the percentage to the left of the z-scores for each of these numbers. To find the z scores, use the formula:
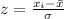
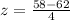 which gives us a z-score of -1. The percentage of numbers to the left of a z-score of -1 is .1586553
which gives us a z-score of -1. The percentage of numbers to the left of a z-score of -1 is .1586553
Now for the other z-score:
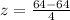 which gives us a z-score of .5. The percentage of numbers to the left of a z-score of .5 is .69146246
which gives us a z-score of .5. The percentage of numbers to the left of a z-score of .5 is .69146246
The lower percentage subtracted from the higher gives the area in question:
.69146246 - .1586553 = .53280716, or as a percentage, 53.3%, choice A.