Question

Ann's first option is a plot of land adjacent to a current park.

The current park is a square, and the addition will increase the width by 200 meters to give the expanded park a total area of 166,400 square meters, This equation represents the area of the first option, where x is the side length of the current square park:

X2 + 200x = 166,400.

Use the most direct method to solve this equation and find the side length of the current square park.

Explain your reasoning for both the solving process and the solution.​

Answer 1

Given:

The equation for the area of the first option is:

`x^2+200x=166400`

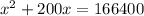
Where x is the side length of the current square park.

To find:

The side length of the current square park.

Solution:

We have,

`x^2+200x=166400`

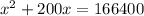
It can be written as:

`x^2+200x-166400=0`

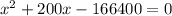
Splitting the middle term, we get

`x^2+520x-320x-166400=0`

`x(x+520)-320(x+520)=0`

`(x-320)(x+520)=0`

`x=320,-520`

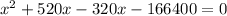
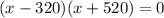
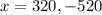
We know that the side length of a park cannot be negative. So, the only possible value of x is 320.

Therefore, the most direct method to solve the given equation is splitting the middle term and the side length of the current square park is 320 meters.