Answer:
Eric can either charge $10 or $40 in order to break even.
Explanation:
Eric has a summer lawn mowing business and the equation:
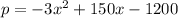
Models his total profit p by charging x dollars per lawn.
We want to determine what price Eric needs to charge in order to break even.
The price Eric charges to break even means that his total profit will be zero. Hence, we can let p = 0 and solve for x. Thu:
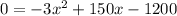
We can divide both sides by -3:
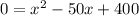
Factor:
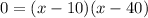
Zero Product Property:
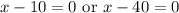
Solve for each case. Hence:
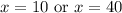
Therefore, Eric can either charge $10 or $40 in order to break even.