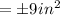Answer:
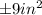
Explanation:
We are given that
Radius of end of a log, r= 9 in
Error,
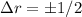 in
in
We have to find the error in computing the area of the end of the log by using differential.
Area of end of the log, A=
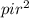
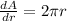
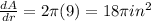
Now,
Approximate error in area

Using the values
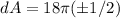

Hence, the possible propagated error in computing the area of the end of the log